| 连续性方程: |
|
| 流体在管道中作稳定流动时,同一时间内流过管道每一截面的流量质量相等。即: |
|
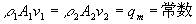
|
式中:ρ1、ρ2--截面1、2上流体的密度 kg/m3
A1、A2--截面1、2的截面积 m2
v1、v2--截面1、2上流体运动速度 m/s qm--质量流量 kg/s |
|
| 如果气体运动速度很低,视为不可压缩的,则: |
|
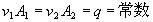
|
| 式中:q--体积流量 m3/s |
| 能量方程: |
| 如果流体流动为稳定流,由能量守恒关系可求得几种形式的能量方程: |
| 不可压缩流体的伯努里方程: |
|
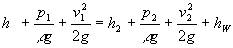
|
式中:h1、h2--截面1、2处的位置高度 m ; p1、p2--截面1、2处的压力 Pa
ρ--流体的密度 kg/m3 ;g--流体的重力加速度 m/s2
v1、v2--截面1、2处的平均流速 m/s2 ;hW--截面1、2间损失掉的水头 m |
| 如果忽略位置高度h的影响,上式乘以ρg可得: |
|
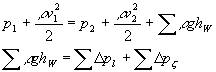
|
式中: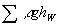 --截面1、2间全部压力损失; --截面1、2间全部压力损失;
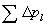 --截面1、2间全部沿程压力损失; --截面1、2间全部沿程压力损失;
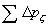 --截面1、2间全部局部压力损失; --截面1、2间全部局部压力损失; |
|
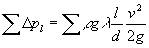
|
| 式中:l、d--管路长度和管内径 m ; |
| λ--管路沿程阻力系数,其值与气体的流动状态和管壁的相对粗糙度有关; |
| 对于层流流动状态的空气和水: |
|
λ=64/Re; |
| 式中:Re--雷诺数,Re=vd/v ; |
| v--气体运动粘度 m2/s |
| 当气体为紊流流动状态时: |
|

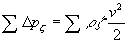
|
| 式中:--f,局部阻力系数; |
| 可压缩气体绝热流动伯努里方程: |
| 如果忽略气体流动式的能量损失和位能变化则: |
|
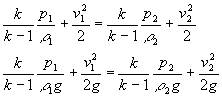
|
| 式中:k--绝热指数; |
| 有机械功的压缩气体能量方程: |
| 若在所研究的管道两截面1-1与2-2之间有流体机械(如压气机、鼓风机或活塞)对单位质量气体做功,则绝热过程能量方程为: |
|
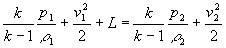
|
| 由此式可得: |
| 绝热过程: |
|
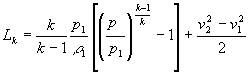
|
| 多变过程: |
|
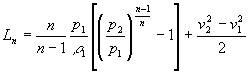
|
| 如果忽略速度v的影响,则得: |
| 绝热过程: |
|
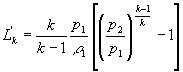
|
| 多变过程: |
|
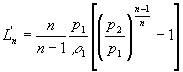
|
| 式中:Lk、Ln--绝热、多变过程流体机械对单位质量气体所作的全功 J/kg |
| L'k、L'n--绝热、多变过程流体机械对单位质量气体所作的压缩功 J/kg |
| 马赫数: |
声速是指声波在空气介质中传播的速度。声波是一种微弱的扰动波。通常将一切微弱扰动波的传播速度都叫声速。
绝热过程声速为: |
|
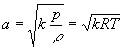
|
| 上式说明,气体的声速决定与介质的温度T,当k=1.4,R=287.1 J/(kg.K)代入式中得: |
|
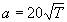 m/s m/s
|
| 当温度为15oC时空其中的声速为a=340 m/s。 |
| 工程上将气流的速度与音速之比称为马赫数,用符号M表示: |
|
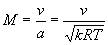
|
| 当气体 v<a 时的流动为亚声速流动; |
| 当气体 v>a 时的流动为超声速流动; |
| 当气体 v=a 时的流动称为声速流动或临界状态。 |
| 流动特性: |
| 气体沿着变截面管道流动时,其流速符合下式: |
|
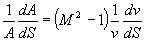
|
| 式中:M=v/a。 |
| 有效截面积: |
| 气动元件、管路等的流通能力可以采用有效截面积S值表示,也可以流量等来表示。 |
| 定义及简化计算: |
| 气体流经节流孔(如阀口)时,由于实际流体存在粘性,使流束的收缩比节流孔名义截面积S0还小,此最小截面积S称为有效截面积。它代表了节流孔的流通能力。显然,节流孔的有效截面积S不等于它的名义截面积S0,而小于S0。二者比值为收缩系数,以a表示: |
|
|
|
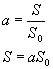
|
|
|
| 气动元件的流通能力也常用S值来表示,即把气体通过气动元件的流动看成类似相同条件下通过节流孔板的流动,这是研究问题的复杂性大为简化。 |
| 对于管路有效截面积S可按下式计算: |
|
S=a'S0 mm2 |
|
|
| 有效截面积测试方法: |
| 气动元件的有效截面即可通过测试确定。下图为电磁换向阀的S值测定装置,由容器放气特性测定放气时间,算出S值: |
|
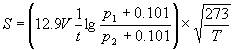
|
| 式中:S--有效截面积 mm2; V--容器的容积 L; |
| t--放气时间 s; T--以绝对温度表示的室温 K; |
| p1--容器内初始压力(相对) MPa p1=0.5MPa ; |
| p2--放气后容器内剩余压力 (相对) MPa p2=0.2MPa; |
| 注:当流动为声速时适用,在亚声速不适用 |
| 系统中多个元件合成的S值 |
| 1.系统中若干个元件并联合成的有效截面积: |
|
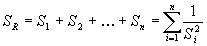
|
| 2.系统中若干个元件串联合成的有效截面积: |
|
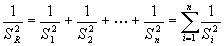
|
| 式中:SR--合成有效截面积; |
| S1、S2……Sn--各元件有效截面积; |

